专题一 函数图象与坐标轴围成的图形面积问题
1.如图，已知两直线y＝－
x＋3和y＝2x－1，求它们与y轴所围成的三角形的面积.
2.如图,直线
与
轴、
轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,且∠BAC=900.假如在第二象限内有一点P
,且△ABP的面积与Rt△ABC的面积相等,求
的值.
3.如图,△AOB为正三角形,点B的坐标为,过点C作直线l交AO于D，交AB于E，且使△ADE和△DCO的面积相等.求直线l的分析式.
专题二 实质应用题
4.某学校要印制一批《学生手册》，甲印刷厂提出：每本收1元印刷费，另收500元制版费；乙印刷厂提出：每本收2元印刷费，不收制版费．
分别写出甲、乙两厂的收费y甲 、y乙与印制数目x 之间的关系式；
问：该学校选择哪间印刷厂印制《学生手册》比较划算？请说明理由．
专题三 一次函数模型的应用
5.某学校的复印任务原来由甲复印社承接，其收费y（元）与复印页数x（页）的关系如下表：
x | 100 | 200 | 400 | 1000 | … |
y | 40 | 80 | 160 | 400 |
|
⑴若y与x满足初中学过的某一函数关系，求函数的分析式；
⑵目前乙复印社表示：若学校先按每月付给200元的承包费，则可按每页0.15元收费.则乙复印社每月收费y（元）与复印页数x（页）的函数关系为__________；
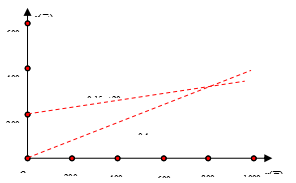⑶在给出的坐标系内画出（1）、（2）中的函数图象，并回答每月复印页数在1200左右应选择什么复印社？
【常识要素】
1.一次函数y=kx+b,当y=0时,得方程kx+b=0,其解是函数图象与x轴的交点的横坐标.
2.不等式kx+b＞0或kx+b＜0的解集,等于一次函数y=kx+b的图象在x轴上方或下方时所对应的x的值.
【温馨提示】
1.借用一次函数与一元一次方程间的关系,可以通过解方程的办法得到一次函数图象与x轴的交点的横坐标,也可以用一次函数的图象求一元一次方程的解,但求出的解一般是近似解.
2.借助一次函数求一元一次不等式的解集,更多的是考查对图象的理解能力,这也说明在学习一次函数时,“数形结合”思想在这一章的重要程度.
3.用一次函数图象解方程或不等式未必简单,但能发现它们之间的内在联系,能直观地看到方程的解与不等式的解在图形中的地方.
【办法方法】
1.因为任何一个一元一次方程都可以转化为ax+b=0的形式,所以解一元一次方程可转化为:当某个一次函数的值为0时,求相应的自变量的值,从图象上看,这等于已知直线y=ax+b,确定它与x轴的交点的横坐标.
2.因为任何一元一次不等式都可以转化为ax+b＞0或ax+b＜0的形式,所以解一元一次不等式可以看作:当一次函数值大于0时,求自变量的相应的取值范围.
3.在用函数图象解一元一次不等式时,对较复杂的不等式应先化简为ax+b＞0或ax+b＜0的形式,然后作出相应的函数图象进行解决,可使解题过程相对简单.
参考答案
1. 解:设直线y＝－x＋3与y轴的交点是A，直线y＝2x－1与y轴的交点是B，两直线的交点是C.在y＝－x＋3中，令x＝0，得y＝3，即点A的坐标为（0，3）；在y＝2x－1中，令x＝0，得y＝－1，即点B的坐标为（0，－1）；由
解得
所以两直线的交点坐标为C（，2），即AB＝4，点C到AB的距离为.则两直线y＝－x＋3和y＝2x－1与y轴所围成的△ABC的面积＝
×4×＝3（平方单位）.
2. 解:由已知可得A
、B,OA=
,OB=1. 
故AB=
.
因此,S△ABC=
×2×2=2.连PO,则S△ABP=S△PBO+S△ABO－S△APO
=
=
.
又S△ABP=S△ABC，
∴，
解得.
3 解:由△ADE和△DCO的面积相等,可知△AOB和△CBE的面积相等, 而△AOB的面积为.设点E的坐标为,则△CBE的面积为2
.
由
,得.
又由直线AB的分析式为,而E在AB上,则
,有
,得E的坐标为.
又由于点C的坐标为,
所以直线l的分析式为
.
4. 解: y甲＝x＋500，y乙＝2x．
当y甲＞ y乙时，
即x＋500＞2x,则x ＜500 ，
当y甲＝y乙时， 即x＋500＝2x,则x＝500，
当y甲＜ y乙时，即 x＋500＜2x, 则x ＞500，
所以该学校印制学生手册数目小于500本时应选择乙厂划算，当印制学生手册数目大于500本时应选择甲厂划算，当印制学生手册数目等于500本时选择两厂成本都一样 ．
5. 解:⑴依据表中的数据可知y是x的正比率函数，设y=kx，将x=100，y=40代入y=kx，得k=0.4，所以函数的分析式为y=0.4x.
⑵y=0.15x+200;
⑶画出函数图象,可得交点坐标为,可看出当复印页数等于800时，两家都可选，当复印页数大于800时则选择乙复印社更划算，当复印页数小于800时则选择甲复印社更划算.因此,当每月复印页数在1200左右时，应选择乙复印社更划算.
